「曲線なのに直線！？そんなことが計算で証明できるなんて！すごい‼︎」
これは、生徒の感想です。

高校２年生数学では、年明けから「微分」の授業入りました。
授業回数はまだ３回ですが、２回目の授業で微分の本質を生徒に味わってもらいました。
その授業展開は資料でご覧ください。

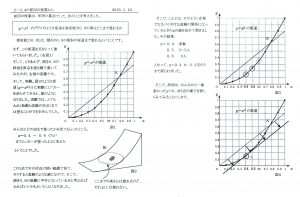
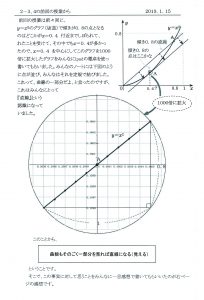
生徒の感想は下記の通りです。（抜粋）
・曲線なのに直線？！そんな事が計算で証明できるなんてすごい！（N）
・曲線を拡大したら直線だった事にびっくりしたし、面白いと思った。（T）
・1000倍に拡大してみたら、グラフが真っ直ぐなことに驚いた。（N)
・曲線が直線に見えてすごいと思った（０）
・地球も真っ直ぐだ！（K）
・普通に見ただけではただの曲線にしか見えなくても、1000倍にしてみると直線ですごく不思議だった。（M）
豊かな表現でこの現象を思い思いに受けとめて表現しています。

１回目　放物線の坂道をミニカー（登坂能力0.4）はどこまで登れるか

２回目　１回目の授業を受けて、予想で絞られた点の付近を1000倍に拡大して見る。
３回目　２回目のことを微分定規（写真を参照してください）を使って、作業によって求めてみる。
グラフを1000倍に拡大して傾きを出した結果と微分定規によって作業で求めた結果は一致しました。

そして、それ以外の各点でのそれぞれの傾きを微分定規を使って求めてみる。
ここから導関数（傾きの関数）が導出されました。このことを微分するといいます。
生徒の写真は、各点での傾きを微分定規で求めているところです。

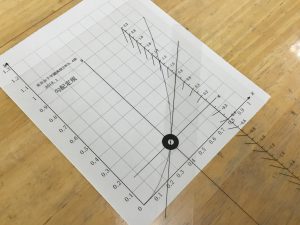
微分定規について

二重の円の中に、グラフの一部分が見えるように透明版を合わせます。
この時でも曲がっているはずの曲線が直線っぽく見えるので、その線上に直線をピッタリ重ねて、傾きを読み取っています。

Tweet